Most of the hydrological designs consider extreme flood flows. Like, in the design of hydraulic structures such as dams, weirs, barrages, bridges, etc one needs maximum flood discharge as well as maximum flood levels. Thus, design flood estimation is a major task for the design of hydraulic structures & river training works. The estimation of runoff from a catchment is a very complex problem. Runoff is generally estimated in the following different forms:
- Annual, seasonal, or monthly runoff
- Extreme low flow or dry weather flow
- Peak flow or flood flow
There are different approaches available for the estimation of runoff. Generally, Runoff estimation is done based on the following methods:
- Statistical or Probabilistic Methods
- Empirical & Regional Methods
- Unit Hydrograph Method
Statistical or Probabilistic methods, used when streamflow data of the study area are available, include graphical methods or flood frequency analysis methods ( Gumbel’s Distribution, Log Pearson Type III, Log-Normal Distribution, etc ). When rainfall data & catchment characteristics of the study area are available, then the empirical & regional methods can be used. For the Unit Hydrograph method to be used, the Unit hydrograph of known duration for a catchment should be available. Here, in this article, I have described about different regional ( WESCS/DHM, DHM, MHSP, PCJ 1996 ) & empirical relations ( Rational, Modified Dicken’s, BD Ricard’s, Synder’s method ) for ungauged stations of Nepal.
WECS/DHM 1990
In the Nepalese context, the Water and Energy Commission Secretariat (WECS)/Department of Hydrology and Meteorology (DHM) developed empirical relationships for analyzing floods of different frequencies. It is the modification of the WESCS approach of 1982.
The formula for 2 year return period is given by
$$Q_{100}=14.63(A_{3000}+1)^{0.7342}$$
where,
Q is design flood in $m^{3}/s$
$A_{3000}$ is basin area($Km^{2}$) below 3000 m elevation.
For other return period,
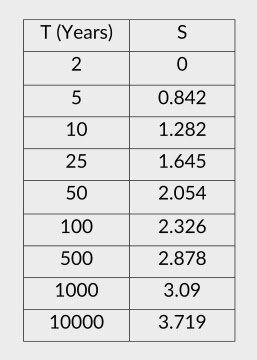
S=Standard Normal Variate
$\sigma=\frac{ln(Q_{100}/Q_{2})}{2.32}$
Table 1 : Values of T & S
The formula for 2 year return period is given by
$$Q_{2}=1.8767(A_{3000}+1)^{0.8737}$$
The formula for 100 year return period is given by$$Q_{100}=14.63(A_{3000}+1)^{0.7342}$$
where,
Q is design flood in $m^{3}/s$
$A_{3000}$ is basin area($Km^{2}$) below 3000 m elevation.
For other return period,
$$Q_{T}=e^{lnQ_{2}+s\sigma}$$
where,S=Standard Normal Variate
$\sigma=\frac{ln(Q_{100}/Q_{2})}{2.32}$
Table 1 : Values of T & S
DHM 2004
The DHM(2004) method is an update to the WESCS/DHM 1990 method.The formula for 2 year return period is given by
$$Q_{2}=2.29(A_{3000})^{0.86}$$
The formula for 100 year return period is given by
$$Q_{100}=20.7(A_{3000})^{0.72}$$
where,
Q is design flood in ($m^{3}/s$)
$A_{3000}$ is basin area($Km^{2}$) below 3000m elevation.
For other return period,
$$Q_{T}=e^{lnQ_{2}+s\sigma}$$where,
S=Standard Normal Variate
$\sigma=\frac{ln(Q_{100}/Q_{2})}{2.32}$
Values of T & S are the same as in table 1.
MHSP 1997
Based on the MHSP method, the flood peak is computed using the relation as below:$$Q=kA^{b}$$
where,
Q is peak flood in $m^{3}/s$
A is basin area in $Km^2$
k and b are constants that depend on the return period T.
Table 2: Values of k & b
k and b are constants that depend on the return period T.
Table 2: Values of k & b
PCJ 1996
This method is an outcome of research conducted by Prof. Dr. Prem Chandra Jha during his Ph.D. studies at a university in Moscow, Russia. The PCJ method calculates design peak flood discharge based on hourly rainfall intensity. The formula for calculation of maximum rainfall discharge is:
where,
Qp = Maximum rainfall design discharge for required exceedance probability (p) in m3/sec
ap= Maximum rainfall design intensity for required exceedance probability (p) in mm/min
ap = ahr.kt, where, ahr = Hourly rainfall intensity for required exceedance probability (p) in mm/min at selected rainfall stations
kt = Reduction coefficient of hourly rainfall intensity (depends on the size of catchment area)
op = Infiltration coefficient of the basin derived as the function of exceedance probability (p)
Φ = Areal reduction coefficient of maximum rainfall discharge (depends on the size of catchment)
F = Catchment area of the drainage basin in sq. km.
KF = Coefficient for unequal distribution of rainfall in different sizes of the basin, captured by one rain.
QS = Discharge by melting of snow can be taken as 0 to 10% of QP in the absence of data.
Rational Method
A rational formula, for flood discharge, takes into account the intensity, distribution and duration of rainfall as well as the area, slope, and permeability of the basin. This method is applicable to small rural catchments with an area not exceeding 12$Km^{2}$ (DHM 2004). A typical rational formula is:
$$Q_{T}=\frac{Ci_{(t_{c},p)}A}{3.6}$$
where,
$Q_{T}$ is the maximum flood discharge in $m^{3}/s$ for the required return period T
C is the runoff coefficient and can be selected based on the type of basin. The values of C for different types of basins are given in table 3.
Table 3: Runoff coefficients
A is the catchment area in $Km^{2}$
$i_{(t_{c},p)}$ is the mean rainfall intensity in mm/hour for probability p and time of concentration $t_{c}$
$i_{(t_{c},p)}$ is the mean rainfall intensity in mm/hour for probability p and time of concentration $t_{c}$
In the absence of data on rainfall intensity, the mean intensity of rainfall ( in cm/hr ) can be estimated by using Sherman equation & coefficients given by Rambabu et.al.
$i_{(t_{c},p)}=\frac{KT^{a}}{(t_{c}+b)^{n}}$
where,
T is return period in years. K, a, b and n are constants for a particular location. For Nepal, these value can be assumed as for Northern India (K = 5.92; a = 0.162; b = 0.5 & n = 1.013). $t_{c}$ is time of concentration (in hour) & can be best estimated by Kripich equation as below:
$t_{c}=0.01947L^{0.77}S^{-0.385}$
where,
$t_{c}$ = time of concentration ( minutes )
L = maximum length of travel of water ( m )
S = Slope of catchment
In the context of Nepal, if 24hr maximum rainfall data are available, then intensity corresponding to the time of concentration can be estimated from Ricard’s method, Mononobe equation, etc.
Modified Dicken's Method
The modified Dicken’s method is an updated version of the Dicken’s method. The irrigation research institute, Roorkee India has done frequency studies on Himalayan Rivers & suggested the following updated relationship to compute Dicken’s constant.
$$Q_{T}=C_{T}A^{3/4}$$
where,
$Q_{T}$=maximum flood discharge($m^{3}/s$) in T years
A=Catchment area($Km^{2}$)
$C_{T}$=modified dickens constant proposed by the Irrigation Research Institute, Roorkee , based on frequency studies on Himalayan rivers
$C_{T}=2.342\log(0.6T)\log(\frac{1185}{p})+4$
$p=100\frac{a+6}{a+A}$
where,
a = perpetual snow area in $Km^{2}$ & T is return period in years.
BD Ricard's Method
This method uses rainfall & basin characteristics during the estimation of floods. The flood discharge is given by:
$$Q=0.222\times(AIF)$$
Where,
The value of I is calculated by iterative process in which initial value of $T_{c}$ in hours is assumed and following calculations are performed.
$$Q=0.222\times(AIF)$$
Where,
A is Basin area in Sq.Km. I is the intensity of rainfall corresponding to the time of concentration & F is the aerial reduction factor.
$F=1.09352-0.066628\ln(A)$The value of I is calculated by iterative process in which initial value of $T_{c}$ in hours is assumed and following calculations are performed.
$I=\frac{R_{TC}}{T_{c}}$
$R_{TC}=0.22127R_{T}T_{c}^{0.476577}$
$K_{R}=0.65I(T_{c}+1)$
$C_{KR}=\frac{0.95632}{K_{R}^{1.4806}}$
$D=1.102\frac{L^{2}}{S}F$
$T_{C3}=DC_{KR}$
$T_{C2}=(\frac{T_{C3}}{0.585378})^{1/2.17308}$
Where, L is the basin length in Km, S is basin slope, $R_{T}$ is 24 hours rainfall for return period T in mm, $T_{C2}$ is the second estimate of time of concentration
Iteration is done with $T_{C}=T_{C2}$ until the difference between them is within 5%