Monthly Flow Estimation | Regional & Empirical Methods in Nepal

Monthly flow estimation of a catchment is a major task for the design of an irrigation system in a required commanded area. We generally estimate runoff as annual or monthly flow, extremely low flow & flood flow. Annual or monthly flow is required for the design of irrigation water requirements whereas extreme low flow & flood flow are determined for the design of hydraulic structures & river training works. Here, in this article, we are mainly concerned with the estimation of monthly flow in the catchment area of study. When long-term flow data of the study are available, we use the frequency analysis method. In absence of such records, we can apply regional & empirical methods to calculate monthly flows.

Frequency Analysis

The design criteria for irrigation schemes in Nepal is 80% reliability of full supply. The value can be obtained using the mean and standard deviation techniques. The 80% reliable flow is obtained as:

$Q_{80}=Q_{mean}-SD * 0.8418$

Example:

$(Q_{80})_{January}=(Q_{mean})_{January}-SD*0.8418$

WECS/DHM 1990

This method was developed by WESCS based on the study of DHM's records, the so-called WESCS/DHM method. The equation developed is given below:

$Q_{mean}= C*(Basin Area)^{A1}$

$*(Basin Area Below 5000+1)^{A2}$

$*(Mean Monsoon Precipitation)^{A3}$

Here, C, A1, A2 & A3 are coefficients whose values are given in Table 1.
Table 1: WECS/DHM predication equation constants

WECS DHM 1990 for Monthly Flow Estimation

MIP Method

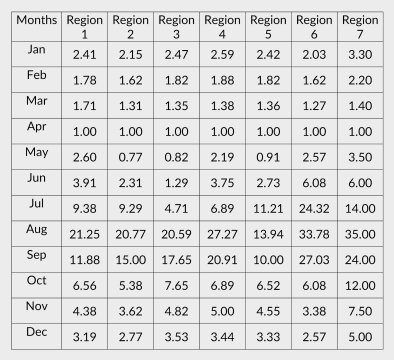
This method uses non-dimensional hydrographs developed for Nepal dividing the whole country into seven different regions & requires at least a single dry weather flow. April flow is obtained by dividing the dry weather flow by corresponding non-dimensional ordinate & then, each ordinate of the required region is multiplied by the April flow to get the monthly hydrograph. Non-dimensional hydrographs are available for

$Q_{80}$ & mean monthly flow.
Table 2: Non-dimensional hydrograph for mean monthly flow

Table 3: Non-dimensional hydrograph for

$Q_{80}$

MHSP 1997

MHSP suggested the following formula to calculate the mean monthly flow of a catchment.

$Q_{mean} = C*(Basin Area)^{A1}$

$*(Mean Monsoon Precipitation)^{A2}$
Table 4: MHSP 1997 predication equation constants

HSC Method

HSC stands for Hydrologically similar catchments which method is applicable only when two catchments have the same yields (discharge/area). If a catchment has long-term flow data & another hydrologically similar catchment has data at least for 3 years, then long-term flow for the second catchment can be calculated from the data of HSC.

Khosla's Method

Khosla (1960) analysed the rainfall, runoff and temperature data for various catchments in India & USA to arrive at an empirical relationship between runoff and rainfall. His relationship for monthly runoff is:

$R_{m} = P_{m} - L_{m}$

Where,